本棋特点
乌合之众象棋,是Infinite chess的一个变种,前名“假装变化无穷,正要为所欲为,才知毫无卵用”象棋。
在发展到V0.8后以后就不叫这么长的名字了,于是就换一个稍微正常一点的名字——乌合之众!
乌合之众:像暂时聚合的一群乌鸦。 比喻临时杂凑的、毫无组织纪律的一群人。但个人的思想很容易被群体所取代,这只需要一个伟大的人带个煽动性节奏。要的就是这种看似杂乱无章而又能够运筹帷幄的感觉。
主要特点是棋盘为无边无际的超立方体,棋子数量无穷,平面分为主战场和其他战场,立面上分为了主位面和其他位面,并通过数学空间坐标的介入使得在比三维更高维度的空间上的战斗成为可能。
虽然规模无穷,但主战场内双方老王的距离却并不远,并且兵的升变条件宽松,大子初始摆放位置可由棋手自行决定并且跨越能力较强,加上可从其他位面或维度天降奇兵,稍不留神就容易陷入被动,节奏紧凑。
设想源自于梦之神翼的网文处女作《昔世幻景交响乐》同世界观的轻小说《颢梦狂想曲》中,由第三高校新棋社社长林栩棋提出的概念棋,在故事设定中,主要用于研究人工智能的深度学习问题,维度灾难问题,以及P对NP问题,用乌合之众象棋中的主位面象征宇宙,主战场象征地球,其他地方都是看似可怕实则无法发挥作用的未知的混沌,讽刺了《昔世幻景交响乐》的设定范围已经编到了全能宇宙,然而故事尚处地球阶段就被腰斩。
本棋缺陷:在可接受的时长内,很有可能无法分出胜负!

(左图为设计历史沿革)
规则详解

“乌合之众”象棋的棋盘是一个由ω条横线、ω条竖线、ω条纵线相交,以及之上ω个维度的超级无限立方阵,ω在数学上表示首个不可数序数,一般人可以把他当成自然数上的无限大就好……
在每一层平面上,棋盘分为有色格和无色格,而格子的颜色也区分了棋盘的区域,绿色为主战场,蓝色为交汇区,红蓝线为跳兵升变区,而其他颜色区域与让子相关。
它看上去像是一个无限向外延伸的国际象棋棋盘,有颜色的格子与没颜色的格子相间拥簇,但根据区域的不同分为各种颜色,并且层层叠叠:其中绝大多数的层面都只有五种颜色,中间四排为天蓝色,边沿还画上了红线和蓝线,两边一边为冷色系一边为暖色系,其中蓝线一边过去四排为灰色,再向外都是紫色,而红线另一边过去四排为肉色,再向外都是橙色……
而在这茫茫多一样的通用层里,只有其中夹着的一层还有其他两种颜色,以天蓝色区域为中轴,多出了一块12排12列的绿色区域,绿色区域的左右两排以及前后六排也改为了浅蓝色,其他的则和通用层差不多。
而棋子则置于立方体之内,或者叫每一层平面的由线框出的方格内。其中坐标(x,y,1)所在的平面为主位面。主位面之外都是100%密度的兵,而主位面的主战场内则会预先空出一些区域由棋手先手决定大子的初始摆放位置。
棋子排布也是以天蓝色区域为中轴,一边是粉红色,一边是深蓝色。前期以兵线互推开辟空间,中期使用分值召唤大子又再次填补空间,当击杀对方老王,将对方大子逼出前线,或占领对方老王的位置等多种方式,都可能但不一定能直接获得胜利。
分值通过吃对方的棋子获得,而雇佣棋子打入,进行高维跃迁,让不同棋子叠加组合,等等行为都需要使用分值,而最后胜负的评判决定都与双方所剩分值多少的对比息息相关。
棋子走法
棋子:
“乌合之众”象棋的棋子形象以国际象棋为基础,分为红蓝双方,棋子种类共设有跳兵、马仔、车夫、相爷、山炮、老王、老后、公子、大哥,共9种,除跳兵外都由玩家选择自行地摆放,按照先后手顺序每方每次挑选一排4个,其中老王、老后、公子、大哥对双方来说都是唯一的,而其他棋子没有数量限制,非选区域的其余位置均被无数跳兵填满。


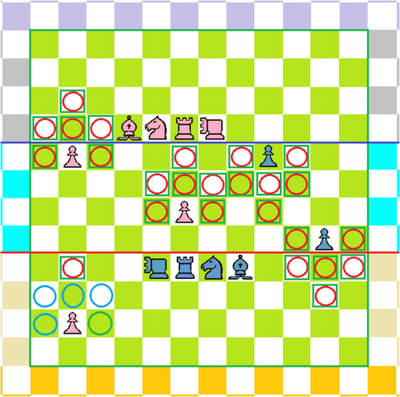
(左图一为开局自选阶段)

(左图二为左图一自选记录及左图三的33手记录)
(左图三为开局前33手)

(左图四为33-66手)

(左图五为66-100手)

(左图六为100-150手)

(左图七为150-200手)
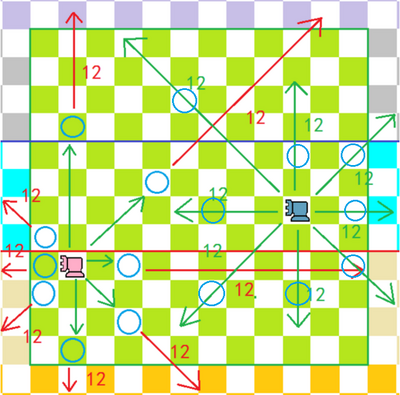
棋子走法吃法:如下图中,绿色方框代表不论中间有没有障碍都能够走到的位置;
红色圆圈代表不论中间有没有障碍都能够吃到的位置;
蓝色圆圈代表任意其他棋子为障碍;
绿色线代表移动的方向,在遇到第一个棋子后停下或跨越最多一个棋子;
红色线代表吃子的方向,在遇到第一个棋子后停下。
跳兵:(分值1分,可升级)
走法:无论第几步都能前进1到2格,并且可以跨越一个棋子;横着向左或向右走一格;斜着向左前方,或右前方一格。
吃法:完全同走法,所有能移动到的位置内有对方棋子,就可以吃掉它而占据该格;
没有吃过路兵,不同于国际象棋。
升级:在到达对方阵线之前一格时,可以选择升级为马仔、车夫、相爷、山炮四个的其中一种,也可以选择暂时不升级,在自己需要的回合进行突然性的升级并正常移动或吃子。
跳兵移动或吃子后升级、跳兵升级后新棋子移动或吃子可以在一手内完成,所以每一个位于对方阵线的跳兵都有着无比强势的下一手,真正可怕的是这样的棋子和机会能有无数个。
类比:相当于能向前跳跃1到2格但无法后退的日本将棋的“金将”。
马仔:(分值3分)
走法:向前后左右直走一到四格,可以越子;斜走一到两格,可以越子;
先左右横走一到三格后再上下直走一格,可以越子;
先上下直走一到三格后再左右横走一格,可以越子;
没有中国象棋中的“蹩马腿”限制。
吃法:先斜走一格,再往外斜吃一格,可以越子;先斜走一格,最后再往原位置外侧横吃或直吃一到两格,可以越子;
向前后左右直接吃到第三格和第四格,可以越子;
类比:以前后左右直走一格为一步,走法为最多四步,吃法为第三步与第四步,无视障碍。
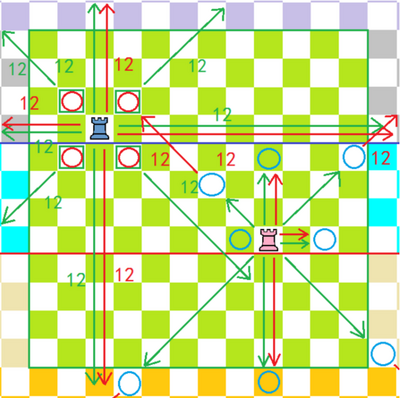
车夫:(分值3分)
走法:横、直、斜都可以走,但不能越子,最远距离原棋子12格。
吃法:斜方向一格;
横、直方向,最远距离原棋子12格,不能越子。
斜方向,己方和对方的棋子中间必须间隔1个棋子(无论对方或己方棋子),最远距离原棋子12格。
类比:相当于日本将棋的“龙王”+仙灵棋的“弩”(斜线炮)。
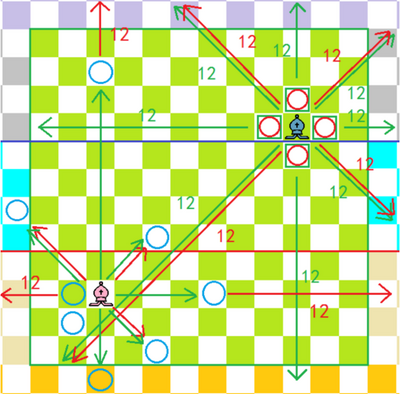
相爷:(分值3分)
走法:横、直、斜都可以走,但不能越子,最远距离原棋子12格。
吃法:横、直方向一格;
斜方向,最远距离原棋子12格,不能越子。
横、直方向,己方和对方的棋子中间必须间隔1个棋子(无论对方或己方棋子),最远距离原棋子12格。
类比:相当于日本将棋的“龙马”+中国象棋的“炮”。

山炮:(分值3分)
走法:横、直、斜都可以走,可以跨越最多1个棋子(无论对方或己方棋子),最远距离原棋子12格。
吃法:横、直、斜方向,己方和对方的棋子中间必须间隔1个棋子(无论对方或己方棋子),最远距离原棋子12格。
类比:相当于八个方向的中国象棋的“炮”+八个方向的韩国象棋的“包”,但没有包不能打包或包不能以包为架子的限制。
老王:(重要)
走法:横、直、斜都可以走,但每次限走一格。
与国际象棋不同,老板是可以被送吃的,即任何被敌方控制的格子,己方老板也能走进去,因为被对方吃掉后不一定会输。
没有王车易位这么一说。
吃法:所有能移动到的位置内有对方棋子,就可以吃掉它而占据该格;
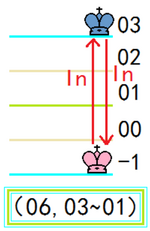
对将:当双方老板位置的x轴坐标相等、或y轴坐标相等、或z轴坐标相等,或者处于同一条直线或斜线或不同位面的同样的平面坐标上,并且当中没有其他棋子阻碍时,轮到行动的一方可以用老板直接吃掉对方老板而占据该格,距离无限。
胜负关系:当己方的老板被对方吃掉,并且自己的剩余分数少于等于对方时,将被判负,否则公子将升级为新的老王。
当自己的老王的初始位置被对方的老王或公子任意一个棋子占据,会被判负。
老后:(分值12分)
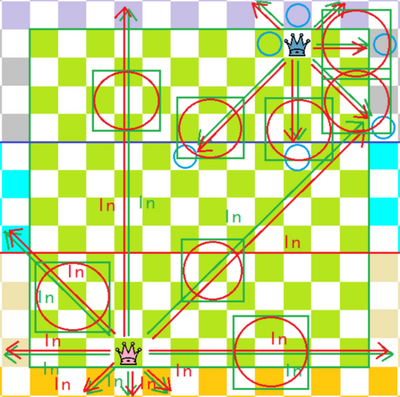
走法:分为两个步骤,第一个步骤:横、直、斜方向都可以走,但不能越子,距离无限;第二个步骤:第一个步骤结束后再以老王的形式,横、直、斜方向再走一格。
吃法:所有能移动到的位置内有对方棋子,就可以吃掉它而占据该格,但两个步骤最多只允许吃一个棋子。
类比:第一个步骤是国际象棋的“皇后”的走吃法,第二个步骤是国际象棋的“国王”的走吃法,两个步骤的先后顺序可以颠倒,但每一回合最多只能吃对方一个子。且吃子后不能再继续移动。
一方的老后被吃后,另一方可以花费12分用其进行雇佣打入1次。
公子:(重要,可升级)
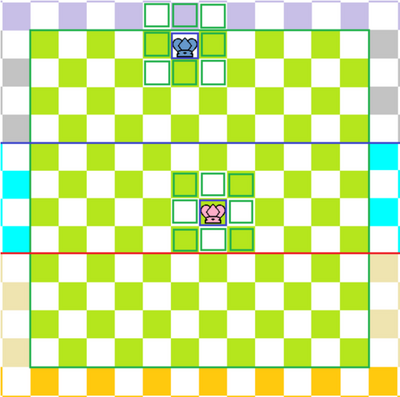
走法:横、直、斜都可以走,但每次限走一格。
吃法:没有吃法,不能吃对方的棋子,但同时自己也是无敌的,不能被对方吃。
升级:当己方的老板被对方吃掉,并且自己的剩余分数多于对方时,公子将升级为新的老王。
胜负关系:当自己的公子的初始位置被对方的老王或公子任意一个棋子占据,会被判负。
当公子升级后的老王再次被对方吃掉,将被判负。
大哥:(分值12分)
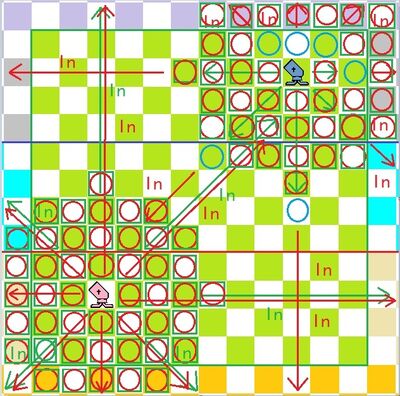
走法吃法:总结就是前面的马仔+车夫+相爷+山炮+走吃用字的融合,但在直线和斜线上走吃和打炮的距离是无限的。
一方的大哥被吃后,另一方可以花费12分用其进行雇佣打入1次。
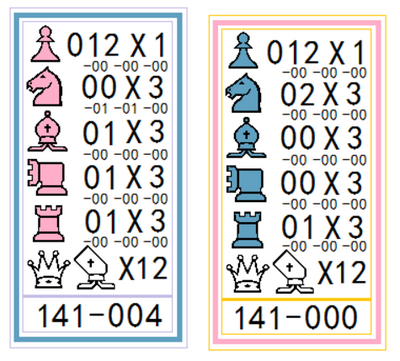
分值系统:(核心)
每一方起始拥有120点分数,吃对方的棋子还会获得相应分数,若吃掉跳兵升变后的棋子,也以升变后的棋子计分。
各种棋子对应的分值如下:跳兵——1分;马仔——3分;相爷——3分;车夫——3分;山炮——3分;老后——12分;大哥——12分。
使用分数:
每一方玩家可以消耗分数雇佣全新的棋子,这些召唤而来的棋子可以随时打入棋盘里的任何没有敌人棋子的坐标位置,不仅可以是空格也可以是已有自己棋子的地方。可以无限购买的棋子有跳兵、马仔、相爷、车夫、山炮,而老后和大哥不能无限购买,只有在吃掉对方的老后或大哥后才可花费12分进行雇佣打入1次。
区别:当打入在主战场之内(绿色区域)要额外消耗1分,而当打入在主战场之外(非绿色区域)则不需要。
除了雇佣打入之外的其他作用:棋子每次在进行高维跃迁(坐标上三维以上的数字发生变动)时要额外消耗1分。
棋子每次进行叠加组合时,在升级线之前需要消耗相等于组合中最高分值棋子所对应的分值,在升级线之后则只需要消耗1分。
胜负关系:当己方的老王被对方吃掉,并且自己的剩余分数少于等于对方时,将被判负;
当己方的剩余分数少于等于0或对方的一半时(比如你只剩50分,而对方大于等于100分,或者你没分了,对方还有分),将被判负;
每种统计吃子得分的大数字下,新增了三串小数字,分别表示该种类棋子的雇佣次数,打入主战场的次数,进行高维跃迁的次数。
三维坐标观察系统:
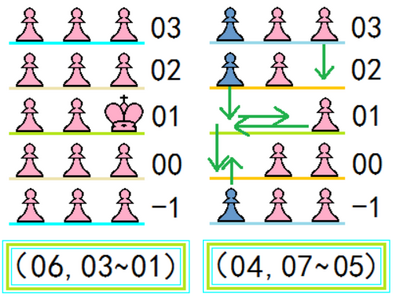
因为棋盘是立方阵,所以除了我们看到的主位面,还有其它无数层平面。
这个界面可以显示在某个指定的(x,y)坐标范围中,z轴棋子的位置。
三维跃迁系统:
一个平面的棋子可以移动到上下相邻一个位面的同一位置(只要那个位置是空格),棋子可以先在自己的平面上移动再跃迁到相邻的平面去,也可以先跃迁之后再在新的平面上移动,但在跃迁的步骤中不允许进行吃子动作。
高维跃迁系统:

但实际上棋盘不止3个维度,而是无限维度,那么怎么体现比三维更高的维度?那么只从数学上去表现,而非空间上。
我们设定一个四维空间里,有无数这样的三维棋盘,而五维空间里又有无数的四维空间,以此类推到无限维度,但只有编号都为01的高维空间里,才有这样的主区域:
而其他维度的任何一个棋盘,则依然是只有无数的兵挤在一起:
那么高维度之间如何完成跃迁呢?我们将这颗坐标标记为(……9,4,1,2,1,1,1,1……)的兵,花费一手以及1分士气值就跃迁到了相邻四维层面的(……9,4,1,1,1,1,1,1……),这一手记做兵(……9,4,1,2,1,1,1,1……)跃迁(……9,4,1,1,1,1,1,1……)。
同样的,相邻的五维位面、六维位面乃至无限维位面,只要再跃迁前后的相应维度在标注数值上相邻即可,并且和三维跃迁一样,棋子可以先在自己的空间中移动再跃迁到相邻的空间中,也可以先跃迁之后再在新的空间中移动,但在跃迁的步骤中不允许进行吃子动作。唯一不同的是,高维跃迁需要消耗1点分值,而三维跃迁不需要,并且完成高维跃迁后可以再接一次三维跃迁,又或者是三维跃迁后再接一次高维跃迁,总之高维跃迁、三维跃迁、平面移动三个行为在每个回合当中互相独立,可自由搭配。
至于X轴标识前面省略号中的又表示什么,在我的设想中那是比高维空间更广阔的集合,等后面我再慢慢介绍。
我们看到,高维跃迁系统是如此的强大,使得“召唤打入系统”显得有些鸡肋,似乎只有大子和位置上的区别了,但实际上在某个位面少一个跳兵的情况下,战线很容易被对手压制,从而导致其他位面的跳兵更容易过前线升级,也随之降临到主战场造成更多的连锁反应。
阵型系统:
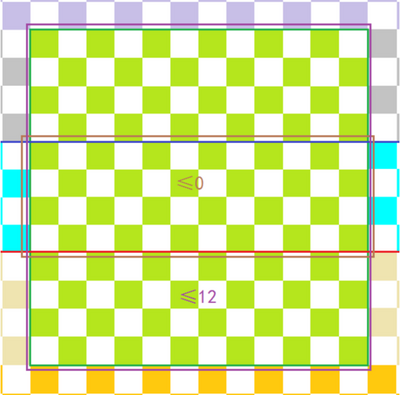
主战场区域内的阵型影响士气,必须寸步不让,否则将一溃千里:
当一方在战场前线内的棋子除了老王和公子,没有其他位置上有棋子时,会被判负;
当一方在主战场内的棋子除了老王和公子,少于或等于12个位置有棋子时,会被判负;
叠子不管多少层棋子都只算一个位置。
自选系统:
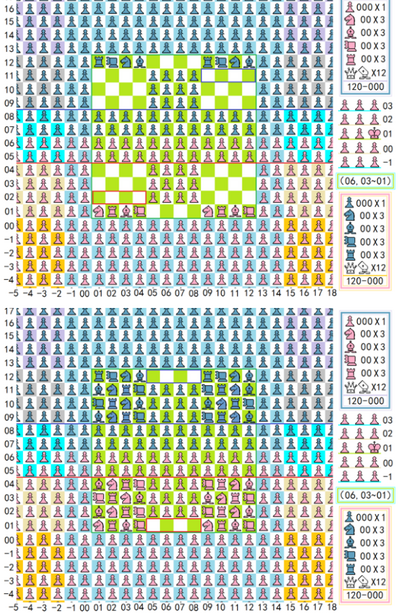
棋局开始前,会把大子的位置空出来,让玩家自己来选择初始摆放方式。
双方先选自己视角的主战场左方最后一排,四个空位,每个空位可选车夫、马仔、山炮、相爷、跳兵之中的一种,进行自由排列,允许重复。若每有一个空格选择跳兵,则选择一方的初始分数+1分。思考时长1分钟,超时则按原先的默认位置安排。
然后是自己视角的主战场右方最后一排,四个空位,还是像上次那样。
之后往前一排,还是从左到右,以此类推到到红线之前。最后是老王、公子、老后、大哥,而这四个不允许重复。
这样还可以根据对方的选择来改变自己的排列,玩出各种套路与反套路。
每次选择棋子排列时,不是双方同时选,而是由先手方(红方)先选,再由后手方(蓝方)后选。
由于现在棋子已经十分强大,先手第一步就可以威胁到大子或准备升级,不管第二步就可以将军,节奏明显加快,这样后手方可以针对先手方的排列,弥补了后行的劣势。
叠加组合系统:
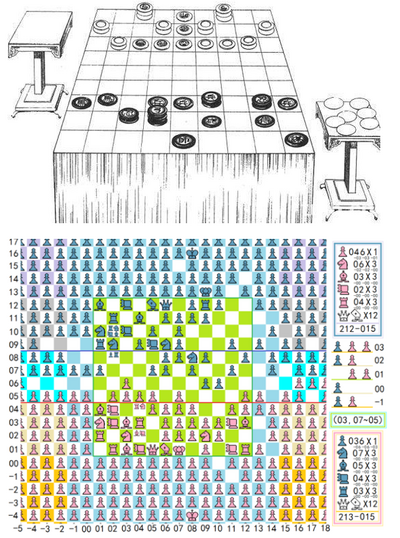
简单来说,就是棋子在移动中可以与己方其他的棋子相叠加。
让大棋盘中的高密度棋子方便活动,同时让不同棋子的能力进行组合,可以统一行动,并在需要的时候又拆分开来,理论上选择与变化也更多。
允许进行叠棋的有:跳兵、马仔、山炮、相爷、车夫、老后、大哥。每次进行叠棋行动都会消耗分数,分为两种情况——升级线之前叠加以及升级线之后叠加:
叠加后的位置在升级线之后的,均只要消耗1分。
叠加后的位置在升级线之前的,分三种情况:叠加前后的双方只有跳兵时消耗1分;而有马仔、山炮、相爷、车夫,没有老后、大哥时消耗3分;当有老后、大哥时则消耗12分。无论是单层叠加入多层,多层走向单层叠加,还是多层与多层叠加,均适用以上耗分规则。
棋子叠起来后可以将能力组合,共同进行移动和吃子,叠加层数没有上限,但也会被对方单个棋子或低层数的棋子通吃串杀,风险与收益并存。雇佣打入系统选择的位置可以与现有的己方棋子直接进行叠加组合。而携带跳兵的多层棋子,在位于升级线后依然可以正常运行升变机制。
叠加组合也可以在三维跃迁以及高维跃迁中使用,可以通过跃迁进行叠加,也可以叠加后进行跃迁,相应的高维跃迁+叠加组合,也需要使用更多的分数。而当多层棋子以统一方式进行高维跃迁时,消耗的分数以多层棋子中分值最高的为标准。
老王、公子因为没有分值设置,所以不能参与叠子,不可以被其他棋子带着到处跑。
拆解组合机制:有叠加就有拆分,意思就是把叠加组合当中的一部分棋子脱离出来行动到别的坐标位置,可以正常移动吃子,跃迁或叠加入其他新的组合当中。每回合只能分出一份,而原先的组合就被一分为二了。
高于ω的集合设定:
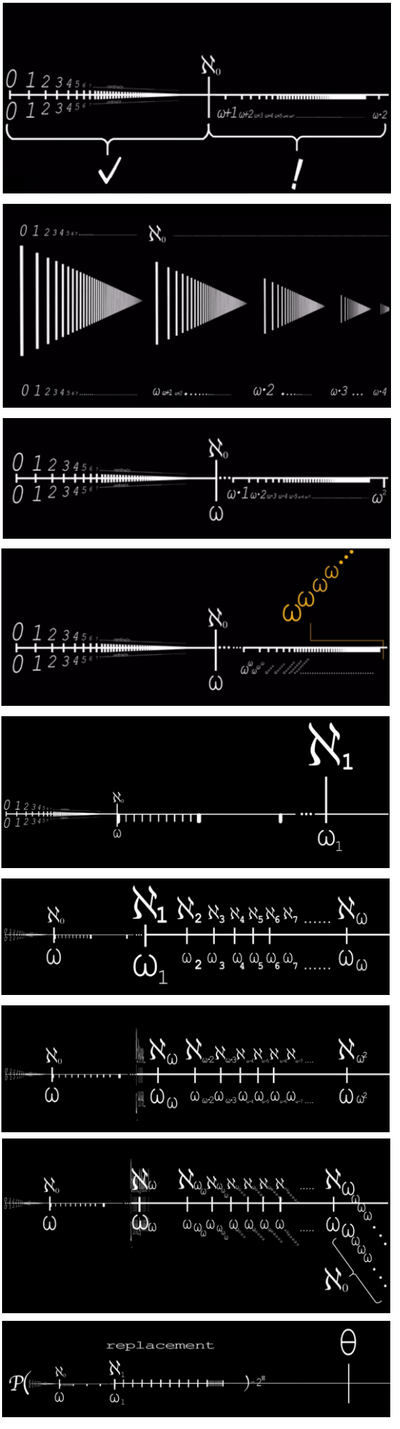
之前所说的X轴标识前面省略号中的又表示什么,比如坐标(……9,4,1,1,1,1,1,1……),我们已经知道Z轴之后表示三维以上的高维空间,而X轴之前表示的集合字数,已经有了成熟的想法,可以将“乌合之众”象棋的变化数从阿列夫零的阿列夫零次方提升至阿列夫一,以下是几张示意图,上述坐标的新表示法为(……0,0,0,0,0——9,4,1,1,1,1,1,1……)
一开始我说了,“乌合之众”象棋的棋盘是一个由ω条横线、ω条竖线、ω条纵线相交的立方阵,那么主战场内的某个棋子坐标可为(9,4,1)
但后面不再局限于立方阵,而是引入了无限维度理论,并依靠坐标系来运作,等于说坐标数量也有ω个,比如说主战场内的某个棋子被计为(9,4,1,1,1,1,1,1……)。
而现在我们又引入了基数的概念,这可以帮助我们的向量数到ω之后。
基数是集合论中刻画任意集合大小的一个概念,两个能够建立元素间一一对应的集合称为互相对等集合。
所以在之前讨论自然数的部分我们只能保证图中打钩部分的存在,但引入集合之后,我们把自然数加到ω之后一一对应,从而最终得到了ω·2!
以此类推,我们通过不断地叠加集合,最终得到了ω^2!
然后我们再通过替代法,把自然数中的1、2、3、4……等,替代到上述中得到的ω^2之中的幂次数,而得到ω^3、ω^4……等,最终又得到ω^ω。
而ω^ω则是一个一层指数塔,要是我们再把自然数中的1、2、3、4……等通过替代法换成那些指数塔的层数,而得到ω^(ω^ω)、ω^(ω^(ω^ω))……等,最终得到ω^(ω^(ω^(ω^(ω^(ω^(ω……)))))),循环ω次。
只有又是以此类推,我们已经做过了3次替代法,要是我们再把自然数中的1、2、3、4……等通过替代法换成做替代法的次数呢?如果从中又发生了自我指涉,那就变成了二阶逻辑,我们再把自然数中的1、2、3、4……等通过替代法换成逻辑的阶数,之后我们还有ω种方法来构成了一个乃至ω个疯狂增长的回路,从而得到了越来越大的基数。
最终,就像我们之前在已知自然数里除了直接设定无法得到ω一样,我们也可以直接设定一个ω1大于所有ω组合的形式。
从而再依靠之前的替代法,又得出ω2、ω3、ω4……一直到ω下标ω。再次替换,又得出ω下标ω·2,ω下标ω·3,ω下标ω·4……一直到ω下标ω^2。
还是跟之前一样,又一次替换得到了ω下标ω下标ω下标ω下标ω下标ω……,循环ω次。
之后我们又有ω种方法来构成了一个乃至ω个疯狂增长的回路,无论我们替代多少次,无论我们用了多少阶逻辑,无论我们又设定了多少个新的基数,除了再引入“不可达基数”外也得不出什么新的东西了,但我在这里暂时并不打算引入那些纯数学概念上的超大基数,而是希望还能看见运用自然数的影子。
了解了上述概念之后,我们现在就可以讲一下,全新的坐标系,类似于(……0,0,0,0,0——9,4,1,1,1,1,1,1……)所表达的含义。
在“——”之后还是跟之前一样,分别表示X轴,Y轴,Z轴,第四维度,第五维度……第ω维度。
而通过上述介绍,我们知道“——”之后的数字不再仅局限于自然数,还可以加入基数来表示,不仅有些坐标可以达到(……0,0,0,0,0——ω+2,ω·2,ω^2,ω^ω,ω↑↑↑↑↑↑……↑↑↑↑↑↑ω,ω2,ω下标ω,ω下标ω^2……)。
甚至于维度数量也可以达到第ω+2维度,第ω·2维度,第ω^2维度,第ω^ω维度,第ω^(ω^(ω^(ω^(ω^(ω^(ω……))))))维度,第ω↑↑↑↑↑↑……↑↑↑↑↑↑ω维度,第ω2维度,第ω下标ω维度,第ω下标ω^2维度,第ω下标ω下标ω下标ω下标ω下标ω……维度,等等等等……
在“——”之前的数字则用来表示“——”之后的按照排序的对应向量,进行了多少次的替换法,“——”每向前间隔一个逗号的数值对应“——”每向后间隔一个逗号的数值:
比如(……0,0,0,0,0——9,4,1,1,1,1,1,1……)里,“——”之前第一个数值为0,则表示“——”之后的第一个数值,也就是X轴的数值没有进行过替换。
而如果是(……0,0,0,0,0——ω+9,4,1,1,1,1,1,1……)里,X轴的数值可以带ω进行表示,所以“——”之前第一个数值依然为0,不需要进行替换。
以此类推,到(……0,0,0,0,0——ω下标ω^2+ω下标ω+ω2+ω↑↑↑↑↑↑……↑↑↑↑↑↑ω+ω^ω+ω^2+ω·2+ω+9,4,1,1,1,1,1,1……)也是同理。
但到了(……0,0,0,0,1——9,4,1,1,1,1,1,1……)里,“——”之前第一个数值为1,则表示“——”之后的第一个数值,也就是X轴的数值用自然数与ω已经无法表示,我们只能进行重新设定来进行了一次替换,替换之后的大基数加上X轴的数值才是它的准确标识。
以此类推,(……0,0,0,1,1——9,4,1,1,1,1,1,1……),(……0,0,1,1,1——9,4,1,1,1,1,1,1……),(……0,1,1,1,1——9,4,1,1,1,1,1,1……),(……1,1,1,1,1——9,4,1,1,1,1,1,1……)……则表示其Y轴、Z轴,第四维,第五维等也进行了相应1次的替换。
那么(……ω下标ω下标ω下标ω下标ω下标ω……,ω2+ω,ω+5,10^10000,1——9,ω+4,ω^5,ω下标ω,1,ω5+ω4·ω3,ω·10^10000,ω下标ω1+ω+10……)就表示X轴数值进行过1次替换再加上9,Y轴数值进行过10的一万次方次数的替换再加上ω+4,Z轴数值进行过ω+5次替换再加上ω^5,第四维向量数值进行过ω2+ω次替换再加上ω下标ω,第五维向量数值进行过ω下标ω下标ω下标ω下标ω下标ω……次替换再加上1,等等以此类推,可以看出是一个非常离散的坐标,而如果实际上每个坐标都是随机的话,将会复杂得无法用可接受的形式进行表达。
那么,关于ω的集合设定有什么用呢?回答:完全没有任何卵用!哈哈哈……想不到吧?
普通玩家依然只要着眼于像这样(9,4,1,1,1,1,1,1……)的坐标就可以了,甚至第四维以上在很多情况下都用不到,只要盯着(9,4,1)这三个维度就行了。
至于前面所扯的ω以后的部分完全不用鸟他,只是我在写小说过程中为了创造“维度灾难”、“P对NP”的矛盾所强行提高逼格的神经病设定!
让子系统:

为了让相对较弱的棋手也有获胜的机会,较强的棋手有时会让n步先或让n级子:
让n步先是让对手先走n步,n可设定为大于等于2的任意自然数。但有限定:不得进行吃子行动,只得进行叠加、跃迁、雇佣打入行动,但在让步过程中进行以上行动不消耗任何分值。但要注意对手可能上来直接吃掉你高分值的叠加组合从而快速获得胜利,所以叠加的位置不建议太靠前。
而在让n级子的情况下,让子必须在开局时将自己一部分的跳兵直接变成对方的,但也不能让对方有机会一步就吃了自己的老王,并保证自己还留有无数的跳兵可用。
不过,因为分值系统的存在,并且“乌合之众”象棋讲究一个“势”。所以并不会因为兵力上的差异而为相对较弱的棋手造成明显的优势。
规定的让子局会按照严重程度递增,每一级都是让出了无限的跳兵,而这个无限的趋势也会越来越大,现罗列如下:
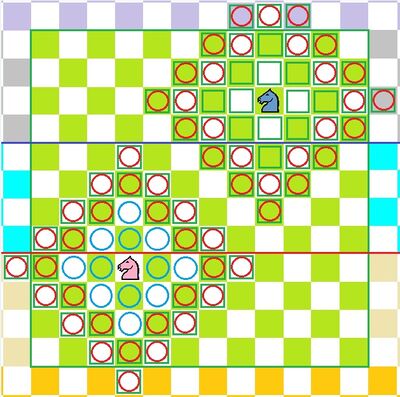
(右图一为相差1级:让前线侧翼两格外前两排的兵;)
(右图二为相差2级:让前线侧翼两格外前两排的兵+主战场侧翼两格外的兵;)
(右图三为相差3级:让前线侧翼两格外前两排的兵+主战场侧翼两格外的兵+主战场后方六排之外除中央四列的兵;)
(右图四为相差4级:让前线侧翼两格外前两排的兵+主战场侧翼两格外的兵+主战场后方六排之外除中央四列的兵+主战场后方侧翼两格外的兵;)
(右图五为相差5级:让前线侧翼两格外前两排的兵+主战场侧翼两格外的兵+主战场后方六排之外除中央四列的兵+主战场后方侧翼两格外的兵+与主位面上下相邻位面的所有的兵;)
(右图六为相差6级:让前线侧翼两格外前两排的兵+主战场侧翼两格外的兵+主战场后方六排之外除中央四列的兵+主战场后方侧翼两格外的兵+除主位面外所有位面的兵;)
(右图七为相差7级:让前线侧翼两格外前两排的兵+主战场侧翼两格外的兵+主战场后方六排之外除中央四列的兵+主战场后方侧翼两格外的兵+第四维到第ω维度在坐标区间[-ω,ω]的兵;)
相差8级以上,就是把上述超过ω部分的维度和坐标上的跳兵也全让了,从第8级开始,每额外再相差一级都是一次替代法或自我指涉,一直到相差ω级乃至前面的ω级概念以上,但这一部分你们可以不用管……
根据需要,让步可与让子配合进行,可以一方同时让n步先和让n级子,也可一方让n级子,而另一方让n步先。
行为配合系统:(并不是新东西,其实算作补充说明)
由于每一回合有大量的行动判断。所以这里主要详细总结了移动、吃子、雇佣打入、跃迁、高维跃迁、叠加组合、拆解组合、跳兵升级,这些行为的配合关系判定。
首先是最高原则:每一手只能对指定的同一坐标位置上的己方棋子进行坐标位置上的改变。
而在每个回合轮到自己行动时,必须遵守以下10点规则:
1、移动后,不能再进行吃子、雇佣打入、拆解组合这些行为。但可以伴随跃迁、高维跃迁、叠加组合、跳兵升级的其中之一的行为进行配合。
2、吃子后,除了跳兵升级外不能再进行任何行为。
3、雇佣打入后,不得再进行移动、吃子、跃迁、高维跃迁、拆解组合。但可以与叠加组合、跳兵升级同时进行。
4、跃迁后,不得再进行吃子、雇佣打入、拆解组合。但可以伴随移动、叠加组合、跳兵升级的其中之一的行为进行配合。
5、高维跃迁后,不得再进行吃子、雇佣打入、拆解组合。但可以伴随移动、叠加组合、跳兵升级的其中之一的行为进行配合。
6、叠加组合后,除了跳兵升级外不能再进行任何行为。
7、拆解组合后,不能再进行雇佣打入,但可以伴随移动、吃子、雇佣打入、跃迁、高维跃迁、叠加组合、跳兵升级的其中之一的行为进行配合。
8、此外,跳兵升级后可以配合以上所有的行为,而同时以上所有行为完毕后也可以再进行跳兵升级。
9、跳兵升级所配合的其他行为都必须是同一格子内的棋子。
10、以上各种行动,每回合每种最多只能进行一次。
胜负及和棋判定条件:
会被判负的条件有8个,满足其中任意一条就会输掉棋局,而对方获胜:
1、当己方的老王被对方吃掉,并且自己的剩余分数少于等于对方,导公子无法升级时,将被判负;
2、当己方的剩余分数少于等于对方的一半时(比如你只剩50分,而对方大于等于100分,或者你0分负分,对方还有分),将被判负;
3、当公子升级后的老王再次被对方吃掉,将被判负;
4、当一方在战场前线内的棋子除了老王和公子,没有其他位置上有棋子时,会被判负;
5、当一方在主战场内的棋子除了老王和公子,少于或等于12个位置上有棋子时,会被判负;
6、当自己的老王或公子的任意一个初始位置被对方的老王或公子任意一个棋子占据,会被判负;
7、当出现重复局面,在主战场12x12的网格中,一模一样的局面出现了6次,而且每次都是同一方走,且没有任何可走棋步差别的时候,同时分值低于对方,会被判负;
8、当出现消极对抗,双方连续60手,没有吃掉过彼此除跳兵以外的大棋子的时候,同时分值低于对方,会被判负。
会被判和的条件有3个,满足其中任意一条双方和棋:
1、当一方Pass一手并提出和棋,另一方同样Pass一手并同意和棋,判为和棋;
2、当出现重复局面,在主战场12x12的网格中,一模一样的局面出现了6次,而且每次都是同一方走,且没有任何可走棋步差别的时候,同时双方分值相等,判为和棋;
3、当出现消极对抗,双方连续60手,没有吃掉过彼此除跳兵以外的大棋子的时候,同时双方分值相等,判为和棋。
经典对局赏析:


自选阶段:棋局开始前,会把大子的位置空出来,让玩家自己来选择初始摆放方式……由先手方(红方)先选,再由后手方(蓝方)后选。这样后手方可以针对先手方的排列,弥补了后行的劣势。
然而我除了把马往中间靠一点有安全感,并不知道怎么放才好,也不知道怎么针对对面,没有什么高深的谋略,就是瞎JB乱放的……
自选结束,对局开始:第一手,先手的我选择跳兵,直接触及到了升级线,这时代入到作为有尊严的后手方,我很不想把这个兵吃掉显得我很没有个性,显得这盘棋空有无限变化,然而就这么不管不顾的话,此子下一手可能升级为任何大子,因为升级都是不消耗步数的,等于这一刻瞬间集合了所有大子的能力,也可能再跳一步将军,虽然也可以到时候再吃,但正面就已经少了两个兵,后续推兵就容易陷入危险,加上无论如何总是要吃的还要浪费一步……那么其他这些地方又有什么用啊?
“我不服,明明还有那么多可以走的地方……可为何就一手都如此扎眼?我就是不想管!反正跃迁也是不消耗步数的,大不了我把其他位面的兵飞到主位面耗下去就好了……”多么可怕的第一步,就让后手的我陷入的长考,看着广袤无垠的多维棋盘,未来的不确定,与迫在眉睫的危机,形成了鲜明的对比,使得迷茫与彷徨淹没了我,最终后手的我决定:“我们和棋吧!” “好啊!双方都不失误的话,可以无限消耗下去,可一旦失手,一溃千里啊!”先手的我如释重负,立马就答应了。 于是,此贴终结!可喜可贺,可喜可贺!
包含了世间一切信息?(尬吹)
科学领域的数字,都不算大到无法想象,用多重指数(多层科学计数法)就可以表达出来。
一阶段:粒子的数目。 1摩尔是6×10^23,而整个可观测宇宙范围内的质子数则是136×2^256(约为1.575×10^79。这个奇怪的表达式是Arthur Eddington给出的),光子数是1.1×10^89,而所有的基本粒子的数目则约为10^97。我们经常说围棋的变化数量超过宇宙的粒子数目就是从此而来。
二阶段:粒子的排列。 小小的围棋盘拥有超过宇宙粒子数的变化就是沾了排列的光。其实只需要很少的粒子,它们的排列数就已经可以超过宇宙中所有基本粒子的数目了。比如6阶魔方的状态数是1.57153×10^116。“微观状态数”就是这样一种排列的概念,而且参与排列的粒子数目更大。整个可观测宇宙的熵大约是10^120,这意味着微观状态数大概是10^(10^120)
三阶段:庞加莱回归时间。 到这个层次,单位已经不重要了(于是会出现“Planck times, millenia, or whatever”)。 一个箱子仅包含一个质量为M普朗克质量的黑洞,那么它的庞加莱回归时间是exp(exp(4πM^2))。 庞加莱证明了一个孤立力学系统经过足够长的时间后,总是可以恢复到初始状态附近,如果该质量为整个宇宙的话,用林德暴胀模型来估计整个宇宙的大小,再代入前面的式子,那就会得到10^10^(10^(10^(10^1.1)))这样的数字,单位是年,也就是经过这么久之后,大概能到另一个轮回的我再一次带你们见证“乌合之众”象棋的时候。
于是,一些脑洞大的人就会想,才这么点大,太无趣了。因为现实世界实在是太小太小了。如果你踏入数学领域,那么你将看到更加巨大的数字。 这些“更加巨大的数字”,我主张分成3类。 第一类,最小的,是可定义、可计算的数,或者能被这样的数限制住的数。代表有葛立恒数,TREE(3)等…… 第二类,更大的,是可定义、不可计算的数,或者能被可定义的数限制住,却没有算法可以计算的数。 第三类,最大的,则是不可定义的数。这里就不一一详细展开了。 但是,这些数字都是有限的,甚至你在自然数里能够真正随机取一个数都是几乎100%几率远远大于它们,所以无论多大都不会超过自然数集合——阿列夫零。 那么,有没有一款屌到不行,变化数量突破这个限制的棋类呢?有的,Infinite chess这一大类以其无可言喻的赖皮方法登顶了棋类变化之最。
其中,我的“乌合之众”象棋更是以通过对无限维空间的数学坐标表现…… 以及通过数学替代和幂集大法不断突破越来越大的极限,即使是在Infinite chess当中也算得上行业翘楚! 没有固定的开局形式,双方的博弈从自选特殊棋子的初始排列就已然白热化…… 分值雇佣系统,高维跃迁系统,让游戏不再局限于平面的推兵,不再局限于一定要杀王,可以从更为宏观的角度经营你的无限王国。
为什么这么吹呢?正是因为它可以模拟了任何粒子在任意维度和空间内的无限排列方式! 数学中对于无限基数的定义是,所有自然数是阿列夫零(ω0),线段上的所有点是阿列夫一(ω1),空间内所有的函数曲线是阿列夫二(ω2),而在这棋的坐标设定中,通过替代法得了远大于这些的基数的集。在其中将无限多的棋子可以排列出任何可能的图案,将图案与字母联系,得到一切信息!
从一开始!无穷无尽,永不重复!在这些数值中,在超越了ω的设定中,包含了任何自然数,实数,虚数,直线,线段,曲线,函数的可能! 你的生日!你的银行密码!你的身份证号码!都暗藏其中! 如果把这些数字转换为字母,就能得到任何的单词,任何的语句,任何的文章,无数种排列组合! 你牙牙学语时发出的第一个音节!你初恋的姓名!你一辈子从始至终的故事!人类成千上万年的历史!乃至宇宙的发展! 无限,到底是什么?超脱不超脱,都没有了意义啊! 那是人说不出来,也想不到的一种境界。其思索的源头来自于一个普遍的困惑,为什么大多的力量体系过半的等级都是在地球上打滚,而后期各种飚升超出宇宙乃至多元? 倘若将各个等级的战力量化,不用明确,就大概的给个上下限的区间,他们想来是会发现前面数以亿万万计,后面就直接跳到无限了的违和了,但是中间的过程和解释呢?
随便翻翻googology就知道在数学里,有着无数在10^100的字节内,只用科学计数法的位数的位数的位数的位数……一直循环也表达不了的各种大数,大部分还是可计算大数,还有高阶图灵机也解决不了的不可计算大数,虽然有限,但也能拿来装逼的啊! 兴许多数人的思维和理解能力大抵也就这样了,满天繁星不计其数或是海水不可斗量,数量过多无法去数或懒得去数,总归是在能直观想到之外放弃思考的略过,这基于人所处的环境而定。 人在习惯上喜欢把能测量的为有限,否则就无限,而一个额外的考量是关于我们的“大”“小”“多”“少”等概念的基础,当我们称呼什么为多时,显然,这已经越过了一个标准线,纵使我们不清楚这条标准线何在,其下则为少。这又如何呢? 在超越于此的大数环境中,其中足以颠覆这些概念。沧海一粟这种用以形容事物之小的概念,若沧海比作宇宙,其一粟也是极大的。那么对于一个我们认知上等效于无限的大数,大于此数的其后所有数的印象感觉辨识等等全都会坍缩至此数,这一个数就能满足人感知上的其后所有了。即比无法想象还无法想象的存在性的成立。
但这种解释还是有点过于繁杂,于是乎设:人类想象不到的存在α与α想象不到的存在β,虽然两者都是人类想象不到的存在,但Level·I·Megaverse 与 Level·II·Megaverse 显然不是同一层次。倘若人类想象不到的存在不仅是α还能代指β甚至是γ,那么Level·All·Megaverse 都将坍缩至 Level·I·Megaverse ,而这是不可能的。 不可说,不可思,不可议,不可到,不可得,不可守,不可在,不可住,不可留,不可来,不可去,不可坏,不可空……慢慢地,汇聚成海的信息无论如何多少物质与能量的重组都只能拼凑出奇形怪状的空间。
从一开始,那是包含了所有自然数的啊列夫零,随后,那是再囊括入无理数的一条直线,接着,那是不断跳跃的无限维度,那是只能通过定义才能达到的不可达基数,马上,那是连数学法则都不允许出现的最大无穷基数,最后,那是超越了绝对无穷,连乘以小于一切无穷小的零都无法阻止的真理之门,不知过了多久,那是超越的一切大道,世间一切真理不过是其梦境一闪而过的无限分之一…… 无限掌握着所有了能量、物质、时间、空间等自然法则,但物理世界从数学概念上讲毕竟是有限!不管是套用修仙的辞藻,还是粉饰自己控制着现实、虚幻、意志、灵魂、精神世界,但再琢磨不透的大数依然不是无穷!
这盘棋,曾经不过只是宇宙大爆炸后,一颗随波逐流的恒星; 这盘棋,曾经不过只是始祖之母的王座中,一道奔腾的瀑布; 这盘棋,曾经不过只是世界之钟指针划过的那一瞬间; 这盘棋,曾经不过只是在宇宙中穿梭前行的辐射微粒; 这盘棋,曾经不过只是作家脑海中迸发出的一丝为了吹逼而吹逼的创作灵感; 这盘棋,曾经不过只是导演在天真孩童时期的一个极限美丽的梦境; 这盘棋……就是一切! 所以,在这个棋盘中,用这些信息做什么,它又有什么用,都取决于你们!
有限和无限的象棋
有限的游戏,其目的在于赢得胜利;无限的游戏,却旨在让游戏永远进行下去。有限的游戏在边界内玩,无限的游戏玩的是边界。有限的游戏具有一个确定的开始和结束,拥有特定的赢家,规则的存在就是为了保证游戏会结束。无限的游戏既没有确定的开始和结束,也没有赢家,它的目的在于将更多的人带入游戏本身,从而延续游戏。
——詹姆斯·卡斯《有限和无限的游戏》

Infinite Chess (无限象棋)不是指某种象棋,而是指一个类型的象棋,其主要特点就是无限大的棋盘和无限多的棋子,可以研究出一些超序数的问题,用于进行游戏的话则一般要满足双方国王的距离有限的条件。
一般的象棋里到和棋也就算结束了,但在无限象棋里,即便没有循环局面或无法行动的情况,离残局也很遥远,玩家往往也是出于自身时间的原因被迫和棋的。
比如最上方示例的那局已经进行了快300手了,双方藏王于深处,分数没有拉开,局面也是扑所迷离,最后不得不协商和棋。但既然无限象棋在有限的时间内难分胜负,那么能否保留和局的局面,以供其他不想经历冗长开局,却依然有兴趣的玩家,接替前人继续进行呢?
因此我有一个大胆的新想法,除了全新的开局,玩家还可以从许多和局库中选取一场,把别人没下完的棋再进行下去,直到分出胜负,或双方同意再次和局继续留给其他人,等于将更多的人带入到这场对局当中,同时也没有确定的开始和结束,至此无限象棋便开始有了无限游戏的雏形。
| 擒王类 | |
|---|---|
| 帝国象棋 ● 龙虎象棋 ● 中西象棋 ● 魔神战棋 ● 未完成页面:王者象棋 ● 合众象棋 ● 箱入将棋 ● 共子象棋 ● 随机军棋 ● 传棋 | |
| 未完成页面:堵路战棋 ● 剑与魔法象棋 ● 乌合之众象棋 | |